Abstract
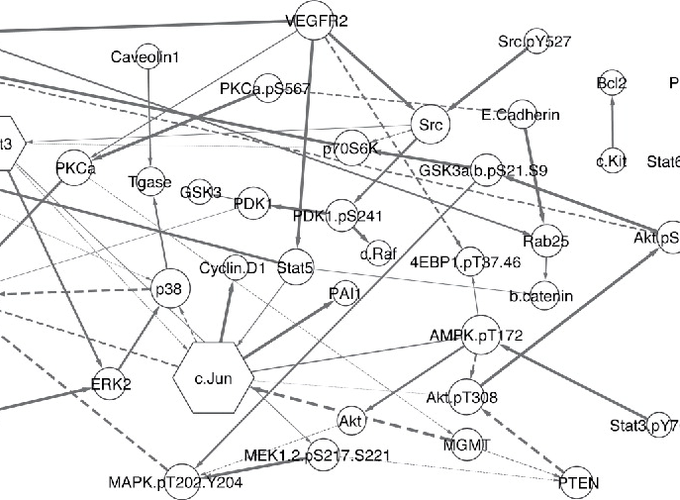
Multi-dimensional data constituted by measurements along multiple axes have emerged across many scientific areas such as genomics and cancer surveillance. A common objective is to investigate the conditional dependencies among the variables along each axes taking into account multi-dimensional structure of the data. Traditional multivariate approaches are unsuitable for such highly structured data due to inefficiency, loss of power, and lack of interpretability. In this article, we propose a novel class of multi-dimensional graphical models based on matrix decompositions of the precision matrices along each dimension. Our approach is a unified framework applicable to both directed and undirected decomposable graphs as well as arbitrary combinations of these. Exploiting the marginalization of the likelihood, we develop efficient posterior sampling schemes based on partially collapsed Gibbs samplers. Empirically, through simulation studies, we show the superior performance of our approach in comparison with those of benchmark and state-of-the-art methods. We illustrate our approaches using two datasets: ovarian cancer proteomics and U.S. cancer mortality. Supplementary materials for this article are available online.