Abstract
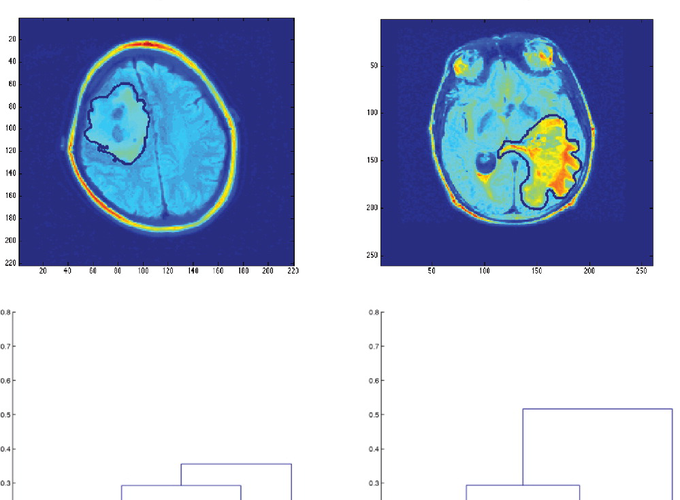
We develop a general statistical framework for the analysis and inference of large tree-structured data, with a focus on developing asymptotic goodness-of-fit tests. We first propose a consistent statistical model for binary trees, from which we develop a class of invariant tests. Using the model for binary trees, we then construct tests for general trees by using the distributional properties of the continuum random tree, which arises as the invariant limit for a broad class of models for tree-structured data based on conditioned Galton–Watson processes. The test statistics for the goodness-of-fit tests are simple to compute and are asymptotically distributed as χ2 and F random variables. We illustrate our methods on an important application of detecting tumor heterogeneity in brain cancer. We use a novel approach with tree-based representations of magnetic resonance images and employ the developed tests to ascertain tumor heterogeneity between two groups of patients. Supplementary materials for this article are available online.